Institute of Geometry

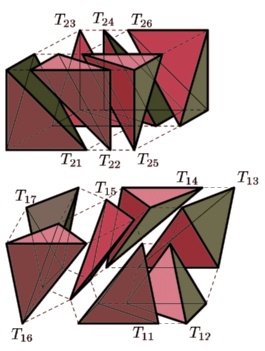
The problem of generalizing ordinary continued fractions to the higher-dimensional case was posed by C. Hermite in 1839. A large number of attempts to solve this problem lead to the birth of several different remarkable theories of multidimensional continued fractions.

We consider the geometrical generalization of ordinary continued fractions to the multidimensional case presented by F. Klein in 1895. Consider a set of n+1 hyperplanes of real (n+1)-dimensional space passing through the origin in general position. Let us choose an arbitrary orthant in the complement to the union of these hyperplanes. The boundary of the convex hull of all integer points except the origin in the closure of the orthant is called the sail. The set of all sails is called the n-dimensional continued fraction associated to the given n+1 hyperplanes. So any sail is a special polygonal surface with vertices in integer points.

Multidimensional continued fractions in the sense of Klein have many connections with other branches of mathematics. For example, J.-O. Moussafir and O. N. German studied the relations between the sails of multidimensional continued fractions and Hilbert bases. H. Tsuchihashi found the connection between periodic multidimensional continued fractions and multidimensional cusp singularities, which generalizes the relationship between ordinary continued fractions and two-dimensional cusp singularities. M. L. Kontsevich and Yu. M. Suhov discussed the statistical properties of the boundary of a random multidimensional continued fraction. The combinatorial topological generalization of Lagrange theorem was obtained by E. I. Korkina and further developed by O. N. German, and its algebraic generalization by G. Lachaud.

We are aiming to establish and to study relations between theory of geometric multidimensional continued fractions from one side and approximation theory and classification of SL(3,Z)-matrices from the other. We are also interested in questions on multidimensional generalizations of Gauss-Kuzmin statistics and other combinatorial properties of the polyhedral faces of sails.

• O. N. Karpenkov and A. M. Vershik. Rational approximation of maximal commutative subgroups of GL(n,R). J. Fixed Point Theory Appl. 7/1 (2010), 241-263. [MR], [doi].
• O. Karpenkov. Continued fractions and the second Kepler law. Manuscripta Mathematica 134 (2011), 157-169. [MR], [doi], [arxiv:0911.2791].
• O. Karpenkov. On determination of periods of geometric continued fractions for two-dimensional algebraic hyperbolic operators. Math. Notes 88/1-2 (2010), 28-38, Russian version: Mat. Zametki, 88(1), (2010), 30--42. [doi].
• O. Karpenkov. On irrational lattice angles. Funct. Anal. Other Math. 2/2-4 (2009), 221-239. [Zbl], [MR], [doi].
• O. Karpenkov. Constructing multidimensional periodic continued fractions in the sense of Klein. Math. Comp. 78/267 (2009), 1687-1711. [MR], [doi], [arxiv:math/0411031].
• O. Karpenkov. Elementary notions of lattice trigonometry. Math. Scand. 102/2 (2008), 161-205. [Zbl], [MR].
• O. Karpenkov. Completely empty pyramids on integer lattices and two-dimensional faces of multidimensional continued fractions. Monatsh. Math. 152/3 (2007), 217-249. [Zbl], [MR], [doi], [arxiv:math/0510482].
• O. Karpenkov. On a criterion for the existence and uniqueness of an integer triangle with given angles. Russian Math. Surveys 61/6 (2006), 1178-1179. [Zbl], [MR], [doi].
• O. Karpenkov. Three examples of three-dimensional continued fractions in the sense of Klein. C. R. Math. Acad. Sci. Paris 343/1 (2006), 5-7. [Zbl], [MR], [doi], [arxiv:math/0601493].
• O. Karpenkov. Classification of three-dimensional multistoried completely hollow convex marked pyramids. Russian Math. Surveys 60 (2005), 165-166. [Zbl], [MR], [doi].
• O. Karpenkov. On two-dimensional continued fractions of hyperbolic integer matrices with small norm. Russian Math. Surveys 59/5 (2004), 959-960. [Zbl], [MR], [doi].
• O. Karpenkov. On the triangulations of tori associated with two-dimensional continued fractions of cubic irrationalities. Funct. Anal. Appl. 38/2 (2004), 102-110, Russian version: Funkt. Anal. Prilozh. 38 (2004), 28-37. [Zbl], [MR], [doi].
• O. Karpenkov. Integer conjugacy classes of SL(3,Z) and Hessenberg matrices. Technical Report 0711.0830v2, ArXiv, September 2009. [arxiv:0711.0830v2].

• V. I. Arnold. Continued fractions. Moscow Center of Continuous Mathematical Education, Moscow, 2002.
• V. I. Arnold. Higher-dimensional continued fractions. Regul. Chaotic Dyn. 3/3 (1998), 10-17, J. Moser at 70 (Russian). [MR].
• O. N. German. Sails and Hilbert bases. Tr. Mat. Inst. Steklova 239/Diskret. Geom. i Geom. Chisel (2002), 98-105. [MR].
• F. Klein. Ueber eine geometrische Auffassung der gewöhnlichen Kettenbruchentwicklung. Nachr. Ges. Wiss. Göttingen Math-Phys. Kl. 3/3 (1895), 352-357.
• F. Klein. Sur une représentation géométrique de développement en fraction continue ordinaire. Nouv. Ann. Math. 15/3 (1896), 327-331.
• M. L. Kontsevich and Y. M. Suhov. Statistics of Klein polyhedra and multidimensional continued fractions. In Pseudoperiodic topology, volume 197 of Amer. Math. Soc. Transl. Ser. 2, pages 9-27. Amer. Math. Soc., Providence, RI, 1999. [MR].
• E. I. Korkina. The simplest 2-dimensional continued fraction. J. Math. Sci. 82/5 (1996), 3680-3685, Topology, 3. [MR].
• E. I. Korkina. Two-dimensional continued fractions. The simplest examples. Trudy Mat. Inst. Steklov. 209/Osob. Gladkikh Otobrazh. s Dop. Strukt. (1995), 143-166. [MR].
• E. Korkina. La périodicité des fractions continues multidimensionnelles. C. R. Acad. Sci. Paris Sér. I Math. 319/8 (1994), 777-780. [MR].
• G. Lachaud. Voiles et polyhedres de Klein. Act. Sci. Ind. Hermann, 2002. 176 pp.
• Z.-O. Mussafir. Sails and Hilbert bases. Funktsional. Anal. i Prilozhen. 34/2 (2000), 43-49, 96. [MR].
• H. Tsuchihashi. Higher-dimensional analogues of periodic continued fractions and cusp singularities. Tohoku Math. J. (2) 35/4 (1983), 607-639. [MR].