Institute of Geometry

This web page and the list of publications below is a snapshot of research done at TU Wien in the years 1998-2005, mostly by Helmut Pottmann and his coauthors.

Helmut Pottmann, Johannes Wallner, Computational Line Geometry, Springer Verlag, Heidelberg, Berlin u.a. 2001. (ISBN 3-540-42058-4, 565 pp. 264 figs., 17 in color)

This book for the first time studies line geometry from the viewpoint of scientific computation and shows the interplay between theory and numerous applications. On the one hand, the reader will find a modern presentation of `classical' material. On the other hand we show how the methods of line geometry enable an elegant approach to many problems whose connection to line geometry is not obvious at first sight.

The geometry of lines occurs naturally in such different areas as sculptured surface machining, computation of offsets and medial axes, surface reconstruction for reverse engineering, geometrical optics, kinematics and motion design, and modeling of developable surfaces. This book covers line geometry from various viewpoints and aims towards computation and visualization. Besides applications, it contains a tutorial on projective geometry and an introduction into the theory of smooth and algebraic manifolds of lines. It will be useful to researchers, graduate students, and anyone interested either in the theory or in computational aspects in general, or in applications in particular.

Supported by project P13648-MAT of the Austrian Science Fund (FWF).

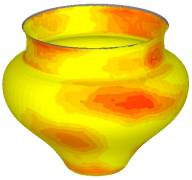
H. Pottmann, M. Hofer, B. Odehnal, and J. Wallner. Line geometry for 3D shape understanding and reconstruction. In T. Pajdla and J. Matas, editors, Computer Vision - ECCV 2004, Part I, volume 3021 of Lecture Notes in Computer Science, pages 297-309. Springer, 2004.

We understand and reconstruct special surfaces from 3D data with line geometry methods. Based on estimated surface normals we use approximation techniques in line space to recognize and reconstruct rotational, helical, developable and other surfaces, which are characterized by the configuration of locally intersecting surface normals.

For the computational solution we use a modified version of the Klein model of line space. Obvious applications of these methods lie in Reverse Engineering. We have tested our algorithms on real world data obtained from objects such as antique pottery, gear wheels, and a surface of the ankle joint.

• M. Hofer, B. Odehnal, H. Pottmann, T. Steiner, and J. Wallner. 3D shape recognition and reconstruction based on line element geometry. In Tenth IEEE International Conference on Computer Vision, volume 2, pages 1532-1538. IEEE Computer Society, 2005, ISBN 0-7695-2334-X.
• B. Odehnal, H. Pottmann, and J. Wallner. Equiform kinematics and the geometry of line elements. Beitr. Algebra Geom. 47/2 (2006), 567-582. [Zbl], [MR].
• B. Odehnal and H. Stachel. The upper talocalcanean join. Technical Report 127, Geometry Preprint Series, Vienna Univ. of Technology, October 2004.
• B. Odehnal. Zur geometrischen Erzeugung linearer Geradenabbildungen. Österreich. Akad. Wiss. Math.-Naturw. Kl. S.-B. II 213 (2004), 43-69.
• B. Odehnal. On isotropic congruences of lines in elliptic three-space. Math. Pannon. 16 (2005), 119-135.
• B. Odehnal. On rational isotropic congruences of lines. J. Geom. 81 (2005), 126-138.
• H. Pottmann, M. Hofer, B. Odehnal, and J. Wallner. Line geometry for 3D shape understanding and reconstruction. In T. Pajdla and J. Matas, editors, Computer Vision - ECCV 2004, Part I, volume 3021 of Lecture Notes in Computer Science, pages 297-309. Springer, 2004, ISBN 3-540-21984-6. [Zbl], [doi].
• H. Pottmann and J. Wallner. Computational Line Geometry. Mathematics + Visualization. Springer, Heidelberg, 2001. ISBN 3-540-42058-4. [Zbl], [MR].
• M. Peternell. G¹-Hermite interpolation of ruled surfaces. In T. Lyche and L. L. Schumaker, editors, Mathematical Methods in CAGD: Oslo 2000, Innov. Appl. Math, pages 413-422. Vanderbilt Univ. Press, Nashville, TN, 2001.
• B. Odehnal and H. Pottmann. Computing with discrete models of ruled surfaces and line congruences. In F. C. Park and C. C. Iurascu, editors, Computational Kinematics, pages 211-226, 2001. Proceedings of the workshop in Seoul, May 19-22, 2001.
• M. Peternell and H. Pottmann. Interpolating functions on lines in 3-space. In A. Cohen, C. Rabut, and L. L. Schumaker, editors, Curve and Surface Fitting: Saint Malo 1999, pages 351-358. Vanderbilt University Press, Nashville, TN, 2000.
• H.-Y. Chen and H. Pottmann. Approximation by ruled surfaces. J. Comput. Appl. Math. 102 (1999), 143-156.
• H. Pottmann, M. Peternell, and B. Ravani. An introduction to line geometry with applications. Computer-Aided Design 31 (1999), 3-16.
• M. Peternell, H. Pottmann, and B. Ravani. On the computational geometry of ruled surfaces. Computer-Aided Design 31 (1999), 17-32.
• H. Pottmann, M. Peternell, and B. Ravani. Approximation in line space: applications in robot kinematics and surface reconstruction. In J. Lenarčič and M. Husty, editors, Advances in Robot Kinematics: Analysis and Control, pages 403-412. Kluwer, 1998.
• H. Pottmann, M. Peternell, and B. Ravani. Contributions to computational line geometry. In D. P. Chi, H. I. Choi, M.-S. Kim, and R. Martin, editors, Differential/Topological Techniques in Geometric Modeling and Processing '98, pages 43-81. Bookplus Press, 1998, ISBN 89-86518-10-0. Proceedings of the Workshop in Pohang, Korea, April 7-8,1998.