TU Graz Logo

Institute of Geometry
Contact   People   Courses & Exams   Events   Research   Lehramtsstudium  

Geometric Spline Theory

This web page and the list of publications below is a snapshot of research done at TU Wien in the years 1993-2005, mostly by Helmut Pottmann and his coauthors.

Speaking of geometric splines means a shift of perspective from numerical analysis to geometry. The many geometric properties of well known spline curves become apparent from a geometric theory at a higher level, which usually reveals more of the inner structure of the functions or curves or surfaces already known from other sources. Another major topic in geometric splines is the generalization of spline curves to manifolds, domains with boundary, and similar nonlinear geometries. Geometric splines are also related to curves defined by intrinsic subdivision processes.

lampe.jpg

J. Wallner, M. Hofer, and H. Pottmann. Fair curve networks in nonlinear geometries ACM SIGGRAPH 2005 Conference Abstracts and Applications, August 2005. Fair webs The Visual Computer 23/1 (2007).

Fair curve networks in nonlinear geometries are an extension of our work on energy-minimizing spline curves in manifolds. Instead of designing with one single curve, we here present a variational approach for the design with an entire network of curves. After a geometric characterization of fair, i.e., energy-minimizing curve networks, we discuss their discretization and computation. Fair curve networks in nonlinear geometries have a variety of applications including surface parameterization, aesthetic remeshing and design of fair surfaces in the presence of obstacles.

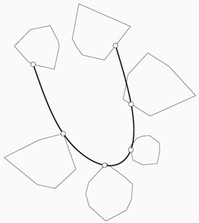
FIGURE MISSING subsets.jpg

Wallner, J., Pottmann, H.: Variational interpolation of subsets. Constr. Approx. 20 (2004), 233-248.

We consider the problem of variational interpolation of subsets of Euclidean spaces by curves such that the L2 norm of the second derivative is minimized. It is well known that the resulting curves are cubic spline curves. We study geometric boundary conditions arising for various types of subsets such as subspaces, polyhedra, and submanifolds, and we indicate how solutions can be computed in the case of convex polyhedra.

FIGURE MISSING geomspl.jpg

Wallner, J., Pottmann, H.: Spline Orbifolds. In: A. Le Méhauté, C. Rabut, L. Schumaker (Eds.) Curves and Surfaces with Applications in CAGD, Vanderbilt University Press, 1997, pp. 445-464.

In order to obtain a global principle for modeling closed surfaces of arbitrary genus, first hyperbolic geometry and then discrete groups of motions in planar geometries of constant curvature are studied. The representation of a closed surface as an orbifold leads to a natural parametrization of the surfaces as a subset of one of the classical geometries S2, E2, and H2. This well known connection can be exploited to define spline function spaces on abstract closed surfaces and use them e.g. for approximation and interpolation problems.


Publications