Geometric Tolerances

This resarch was performed at TU Wien, and was supported by the Austrian Science Foundation (FWF) under grant No. P15911

M. Hofer, G. Sapiro, and J. Wallner. Fair polyline networks for constrained smoothing of digital terrain elevation data. IEEE Trans. Geosc. Remote Sensing 44/10/2 (2006), 2983-2990.

We present a framework which uses fair polyline networks for smoothing digital terrain elevation data with guaranteed error bounds and feature preservation. The algorithm is capable of smoothing the terrain data with tolerance cylinders of different sizes. These flexible tolerances have two advantages in particular: (i) we can preserve features present in the data by reducing the size of the tolerance cylinders in feature areas, (ii) the algorithm can be used to fill holes present in the original data during the smoothing process. Single contour lines are smoothed via processing of a small neighborhood of that contour line.

H.-P. Schröcker and J. Wallner: Curvatures and Tolerances in the Euclidean Motion Group. Results Math. 47 (2005), 132-146.

We investigate the action of imprecisely defined affine and Euclidean transformations and compute tolerance zones of points and subspaces. Tolerance zones in the Euclidean motion group are analyzed by means of linearization and bounding the linearization error via the curvatures of that group with respect to an appropriate metric.

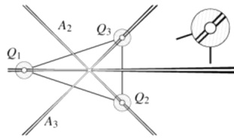J. Wallner, H.-P. Schröcker, and S. Hu. Tolerances in geometric constraint problems. Reliab. Comput. 11, 234-251 (2005). We study error propagation through implicit geometric problems by linearizing and estimating the linearization error. The method is particularly useful for quadratic constraints, which turns out to be no big restriction for many geometric problems in applications. This work is supported by the Austrian Science Foundation (FWF) with grant No. P15911

Wallner, J., Krasauskas, R., Pottmann, H.: Error Propagation in Geometric Constructions, Computer-Aided Design 32 (2000), 631-641.

In this paper we consider error propagation in geometric constructions from a geometric viewpoint. First we study affine combinations of convex bodies: This has numerous examples in spline curves and surfaces defined by control points. Second, we study in detail the circumcircle of three points in the Euclidean plane. It turns out that the right geometric setting for this problem is Laguerre geometry and the cyclographic mapping, which provides a point model for sets of circles or spheres.

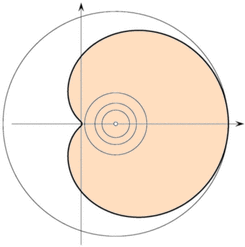
Farouki, R., Pottmann, H.: Exact Minkowski Products of N Complex Disks. Reliable Computing 8, 2002, 43-66.

An exact parameterization for the boundary of the Minkowski product of N circular disks in the complex plane is derived. When N > 2, this boundary curve may be regarded as a generalization of the Cartesian oval that bounds the Minkowski product of two disks. The derivation is based on choosing a system of coordinated polar representations for the N operands, identifying sets of corresponding points with matched logarithmic Gauss map that may contribute to the Minkowski product boundary. In certain applications, the availability of exact Minkowski products is a useful alternative to the naive bounding approximations that are customarily employed in complex circular arithmetic.

Publications

• J. Wallner. Note on curve and surface energies. Comput. Aided Geom. Des 24 (2007), 494-498. [MR], [doi].
• M. Hofer, G. Sapiro, and J. Wallner. Fair polyline networks for constrained smoothing of digital terrain elevation data. IEEE Trans. Geosc. Remote Sensing 44/10/2 (2006), 2983-2990. [doi].
• Q.-M. Yang and J. Wallner. Asymptotic analysis of implicit tolerance problems. Math. Pannon. 16/2 (2005), 263-285. [MR].
• Q.-M. Yang. Geometric contributions to tolerance analysis. PhD thesis, Vienna University of Technology, 2005. Advisor: Johannes Wallner.
• J. Wallner and Q.-M. Yang. Swept volumes of many poses. In M. Desbrun and H. Pottmann, editors, SGP 2005: Third Eurographics Symposium on Geometry processing, pages 161-170. Eurographics Association, 2005, ISBN 3-905673-24-X.
• H.-P. Schröcker and J. Wallner. Geometric constructions with discretized random variables. Reliab. Comput. 12/3 (2006), 203-223. [Zbl], [MR], [doi].
• H.-P. Schröcker and J. Wallner. Curvatures and tolerances in the Euclidean motion group. Results Math. 47 (2005), 132-146. [MR].
• S.-M. Hu and J. Wallner. A second order algorithm for orthogonal projection onto curves and surfaces. Comput. Aided Geom. Design 22/3 (2005), 251-260. [MR], [doi].
• J. Wallner, H.-P. Schröcker, and S.-M. Hu. Tolerances in geometric constraint problems. Reliab. Comput. 11 (2005), 235-251. [Zbl], [MR], [doi].
• J. Wallner. On a problem of elementary differential geometry and the number of its solutions. J. Geometry Graphics 10 (2006), 155-160. [Zbl], [MR].
• S.-M. Hu and J. Wallner. Error propagation through geometric transformations. J. Geom. Graphics 8/2 (2004), 171-183. [Zbl], [MR].
• J. Wallner. Existence of set-interpolating and energy-minimizing curves. Technical Report 111, Institute of Geometry, 2003-2004.
• H. Mühlthaler and H. Pottmann. Computing the Minkowski sum of ruled surfaces. Graphical Models 65 (2003), 369-384.
• R. T. Farouki and H. Pottmann. Exact Minkowski products of n complex disks. Reliab. Comput. 8 (2002), 43-66.
• H. Pottmann, B. Odehnal, M. Peternell, J. Wallner, and R. Ait Haddou. On optimal tolerancing in Computer-Aided Design. In R. Martin and W. Wang, editors, Geometric Modeling and Processing 2000, pages 347-363. IEEE Computer Society, Los Alamitos, Calif., 2000, ISBN 0-7695-0562-7.
• J. Wallner, R. Krasauskas, and H. Pottmann. Error propagation in geometric constructions. Computer-Aided Design 32 (2000), 631-641.
• H. Pottmann. General offset surfaces. Neural, Parallel & Scient. Comput. 5 (1997), 55-80.